Next: Conclusions
Up: No
Title Previous: Mathematical
Analysis
Stability Analysis
Next we linearize the canonical system to analyze the stability behavior
of the steady state. This yields
where 
and 
is
the Jacobian evaluated at the steady state 
. The Jacobian is given by the 
matrix:
where the derivatives of the functions have to be evaluated at steady
state.
According to Ref. 9, the eigenvalues of Jacobian matrices of the following
type:
are given by:
where 
is the sum of the determinants 
Moreover such a Jacobian has a pair of purely imaginary eigenvalues
if and only if the relations
hold.
For our model the constant
and the determinant 
are given by
In the remainder of this section we make use of a linear utility function 
and assume 
.
Then we obtain:
The bifurcation condition (28) is equivalent to
Choosing 
as bifurcation parameter the critical value 
can be calculated from (34)
Note that the steady state values of
do not depend on the parameter .
By choosing the parameter values 
, 
, 
and
the function 
,
we can calculate the steady state and if 
holds, then the critical value 
can be calculated from (34). In this case the Jacobian evaluated at the
equilibrium has a pair of purely imaginary eigenvalues 
.
Moreover, the crossing velocity
Therefore we conclude that isolated periodic solutions will exist either
for 
or 
.
To determine the stability of the cycles and the direction of the bifurcation
further computations either analytically or numerically are necessary.
As the analytical proof of the stability of cycles generated by a Hopf
bifurcation is rather cumbersome even in very simple models (see, e.g.,
Ref. 11), we will present a numerical example leading to a stable cycle.
Specify the following functions 
Furthermore choose the parameter values 
, 
and 
. For
these values the steady state is given by 
According to (35) the critical value 
can be computed. To determine the stability of cycles and the direction
of the bifurcation further numerical investigations with the code BIFDD
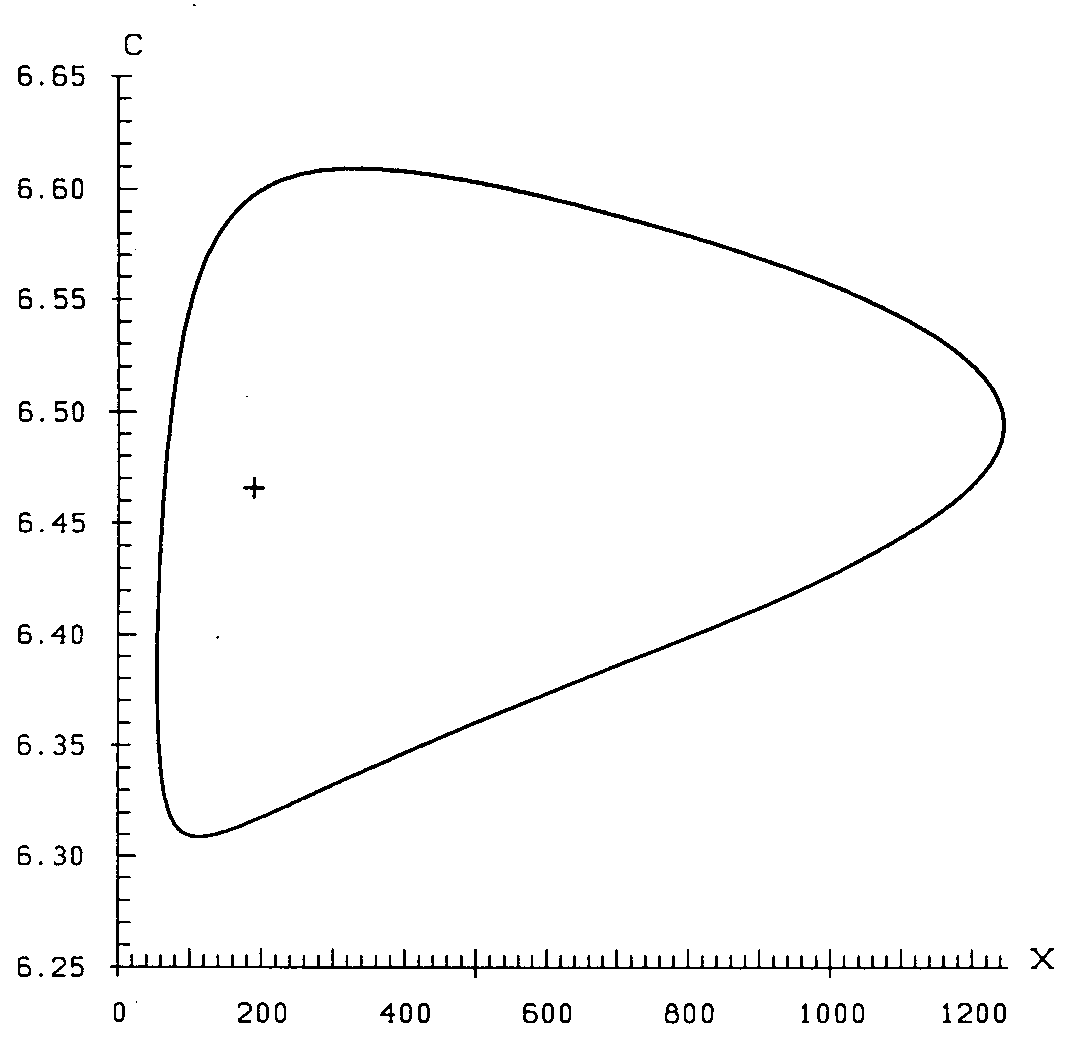
(see Ref. 12) were carried out. It turned out that stable cycles occur
for 
. Using
the boundary value problem solver COLSYS (see Refs. 13 and 14) a stable
limit cycle could be found, e.g., for 
.
This cycle in the 
-plane
is illustrated in figure 1.
Figure 1: Cycle of fear for Vampires