
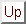

where
stock of
humans in an isolated Transylvanian community
number
of vampires
death rate
of vampires due to contact with sunlight, crucifixes, garlic, and vampire
hunters
growth
rate of the human population
contact
coefficient.
While
and
are
time functions,
,
and
are
constant positive parameters. The term
in (1) and (2) means that each time a vampire meets a human being the former
extracts blood from the latter and, by doing so, turns him into a vampire.
Clearly this predator-prey model leads to cyclical time paths of
and
.
In Ref. 3, the optimal bloodsucking strategy for the vampire population
has been determined. For this it has been assumed that the vampire community
decides about the control variable ,
where:
bloodsucking
rate (number of consumed humans) per vampire
utility
derived by the average vampire from blood consumption at rate
vampires'
discount rate.
This implies that the objective function (total utility per vampire) is
which has to be maximized w.r.t. the controlled state equations
By defining the stock of humans per vampire
the system (4), (5) can also be written as
In Ref. 3, this control problem was solved in the three different cases of
In Ref. 4, the analysis of the one state variable vampirism problem was completed by solving the case of a convex-concave utility function and by showing, that a suitable state transformation can be used to establish the optimality of the candidate solution obtained by the maximum principle. Note that in the original formulation of the Transylvanian problem the usual sufficiency conditions are not satisfied.
In all these formulations, however, the resulting monotonic state trajectories and bloodsucking rates are not in accordance with empirical evidence. It is well known that the appearances of vampires follow a typical cyclical behavior. Therefore this paper's purpose is to extend the model in such a way that more realistic cyclical bloodsucking patterns are optimal.
One way of doing so would be to consider case (c) where chattering was optimal. By introducing some inertia by imposing adjustment costs on the consumption rate this cyclical behavior could be obtained as in Ref. 7 or Ref. 8. However-strictly speaking-the cyclical solutions obtained can then only be called candidates for optimal solutions since the sufficiency conditions are not satisfied.
Thus we choose to follow a path motivated by Refs. 9 and 10, in which we consider a purely concave model where the sufficiency conditions are satisfied and where the appearance of cycles can be proven analytically. In particular, we assume that the change of the consumption rate induces costs and that the vampire community also derives some utility from possessing humans and not only from consuming them.
Let us thus define:
rate of
change of the consumption (bloodsucking) rate
adjustment
costs caused by changes of the consumption rate
utility
derived by the average vampire from having available a resource of x humans
per vampires.
The extended optimal control problem becomes:
subject to
Unfortunately, the Hamiltonian is not concave in the state vector
because of the term
in (8). This problem can, however, be overcomed by applying the state transformation
used in Ref. 4. Define the transformed resource stock
by
then the problem (7) - (9) is equivalent to
subject to
where
and
.
Let us assume that the utility functions
and
are
concave in
and
, respectively,
and that the adjustment cost function
is convex. Then this is a purely concave model and all cross partials are
zero. The investigation of the canonical system is therefore comparably
simple. In particular, the stationary points can be computed and using
the Hopf bifurcation theorem it can be shown that cyclical solutions exist.
These and their stability properties can then be computed numerically for
some parameter values.